[TOC]
BitSet
在分析原理之前,我们先抛出个概念,如下图,第一行我们用来写二进制数,第二行则是对应二进制数为1的十进制数,刚好我们发现,自然数0,1,2…n,均存在对应的一个独立位置的二进制数。那么为了更好表示自然数存在,我们在其对应的二进制数位置上用1标识存在,反之0则不存在。
例如:针对数组[0,2,3],我们用二进制数1101表示,即3,2,0存在,1不存在。
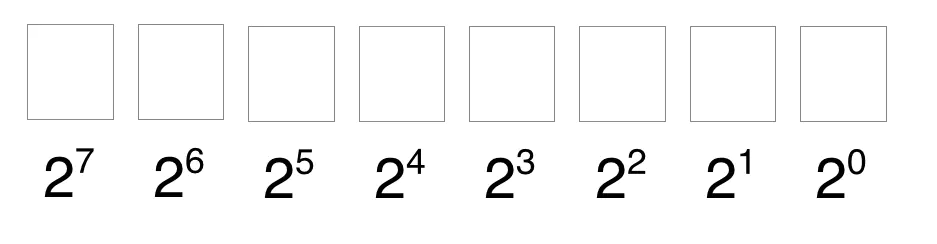
原理
Java的BitSet使用一个Long(一共64位)的数组中的每一位(bit)是否为1来表示当前Index的数存在不。但是BitSet又是如何实现的呢?其实只需要理解其中的两个方法:
- set
- get
就能够理解BitSet的实现原理是什么了。
set
先看源代码:
public void set(int bitIndex) {
if (bitIndex < 0)
throw new IndexOutOfBoundsException("bitIndex < 0: " + bitIndex);
int wordIndex = wordIndex(bitIndex);
expandTo(wordIndex);
words[wordIndex] |= (1L << bitIndex); // Restores invariants
checkInvariants();
}
private static int wordIndex(int bitIndex) {
return bitIndex >> ADDRESS_BITS_PER_WORD;
}
这里ADDRESS_BITS_PER_WORD的值是6,那么最先想到的问题就是:为什么是6呢?而不是其他值呢?
答案其实很简单,还记得在最开始提到的:BitSet里使用一个Long数组里的每一位来存放当前Index是否有数存在。
因为在Java里Long类型是64位,所以一个Long可以存储64个数,而要计算给定的参数bitIndex应该放在数组(在BitSet里存在类型为long[]的word的实例变量里)的哪个Long里,只需要计算:bitIndex / 64即可,这里正是使用>>来代替除法(因为位运算要比除法效率高),而64正好是2的6次幂,所以ADDRESS_BITS_PER_WORD的值是6。
通过wordIndex函数就能计算出参数bitIndex应该存放在words数组里的哪一个Long里。
expandTo
private void expandTo(int wordIndex) {
int wordsRequired = wordIndex+1;
if (wordsInUse < wordsRequired) {
ensureCapacity(wordsRequired);
wordsInUse = wordsRequired;
}
}
从上面已经知道在BitSet里是通过一个Long数组(words)来存放数据的,这里的expandTo方法就是用来判断words数组的长度是否大于当前所计算出来的wordIndex(简单的说,就是能不能存的下),如果超过当前words数组的长度(记录在实例变量wordsInUse里),也即是存不下,则新加一个long数到words里(ensureCapacity(wordsRequired)所实现的。)。
Restores invariants
words[wordIndex] |= (1L << bitIndex); // Restores invariants
这一行代码可以说是BitSet的精髓了,先不说什么意思,我们先看看下面代码的输出:
System.out.println(1<<0);
System.out.println(1<<1);
System.out.println(1<<2);
System.out.println(1<<3);
System.out.println(1<<4);
System.out.println(1<<5);
System.out.println(1<<6);
System.out.println(1<<7);
输出是:
1
2
4
8
16
32
64
128
这个输出看出规律没有?就是2的次幂,但是还是不太好理解,我们用下面的输出,效果会更好:
System.out.println(Integer.toBinaryString(1<<0));
System.out.println(Integer.toBinaryString(1<<1));
System.out.println(Integer.toBinaryString(1<<2));
System.out.println(Integer.toBinaryString(1<<3));
System.out.println(Integer.toBinaryString(1<<4));
System.out.println(Integer.toBinaryString(1<<5));
System.out.println(Integer.toBinaryString(1<<6));
System.out.println(Integer.toBinaryString(1<<7));
输出是:
1
10
100
1000
10000
100000
1000000
10000000
从而发现,上面所有的输出力,1 所在的位置,正好是第1,2,3,4,5,6,7,8(Java数组的Index从0开始)位。而BitSet正是通过这种方式,将所给的bitIndex所对应的位设置成1,表示这个数已经存在了。这也解释了(1L << bitIndex)的意思(注意:因为BitSet是使用的Long,所以要使用1L来进行位移)。
搞懂了(1L << bitIndex),剩下的就是用或运算|来将当前算出来的和以前的值进行合并了words[wordIndex] |= (1L << bitIndex);。
剩下的checkInvariants就没什么好解释的了。
get
搞懂了set方法,那么get方法也就好懂了,整体意思就是算出来所给定的bitIndex所对应的位数是否为1即可。先看看代码:
public boolean get(int bitIndex) {
if (bitIndex < 0)
throw new IndexOutOfBoundsException("bitIndex < 0: " + bitIndex);
checkInvariants();
int wordIndex = wordIndex(bitIndex);
return (wordIndex < wordsInUse)
&& ((words[wordIndex] & (1L << bitIndex)) != 0);
}
计算wordIndex在上面set方法里已经说明了,就不再细述。这个方法里,最重要的就只有:words[wordIndex] & (1L << bitIndex)。这里(1L << bitIndex)也已经做过说明,就是算出一个数,只有bitIndex位上为1,其他都为0,然后再和words[wordIndex]做&计算,如果words[wordIndex]数的bitIndex位是0,则结果就是0,以此来判断参数bitIndex存在不。